Entendiendo los LSTM

Las redes de Memoria a Largo y Corto Plazo, o LSTM, son una forma especializada de Redes Neuronales Recurrentes (RNN) diseñadas para abordar las limitaciones de las RNN tradicionales en el manejo de dependencias a largo plazo. Introducidas por Hochreiter y Schmidhuber en 1997, los LSTM se han convertido en una piedra angular en las tareas de modelado de secuencias.

La principal innovación de los LSTM radica en su capacidad para retener información durante períodos de tiempo prolongados. Esto se logra a través de una estructura celular única equipada con puertas que regulan el flujo de información. Estas puertas permiten a los LSTM olvidar, retener o pasar información al siguiente paso temporal de manera selectiva, lo que los hace altamente efectivos para tareas que requieren retención de contexto, como la predicción de series temporales, el modelado de lenguaje y el reconocimiento de voz.

Características Clave

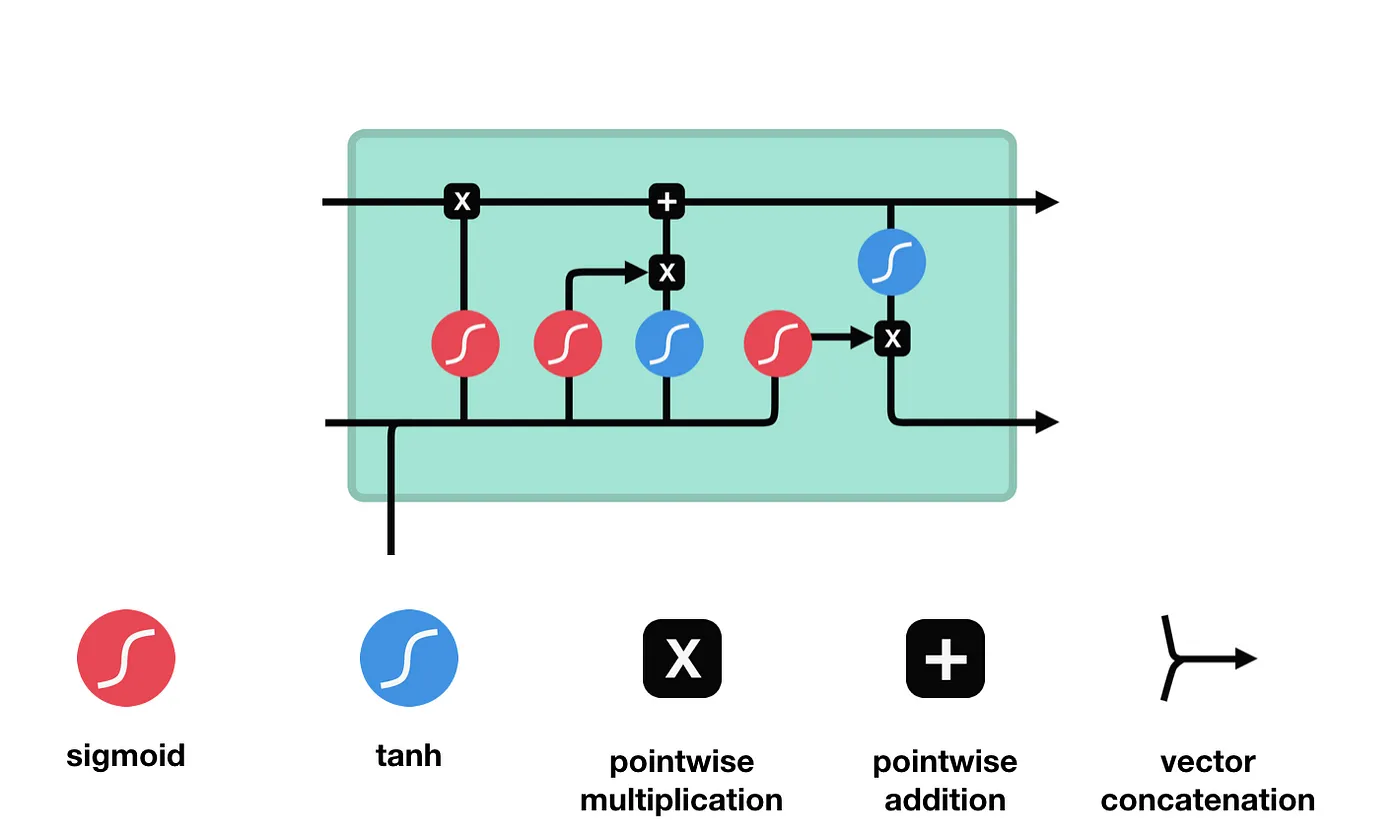
Los LSTM están diseñados para superar el problema del gradiente que desaparece que afecta a las RNN tradicionales durante el entrenamiento. Su arquitectura distintiva incluye:

• Puerta de Olvido: Decide qué información descartar del estado de la celda.
• Puerta de Entrada: Determina qué nueva información agregar al estado de la celda.
• Puerta de Salida: Regula qué información se debe outputear en cada paso temporal.

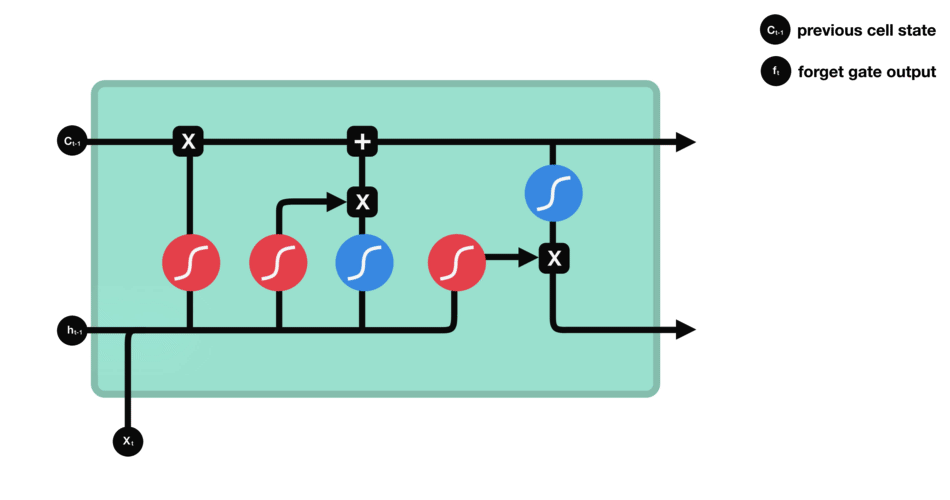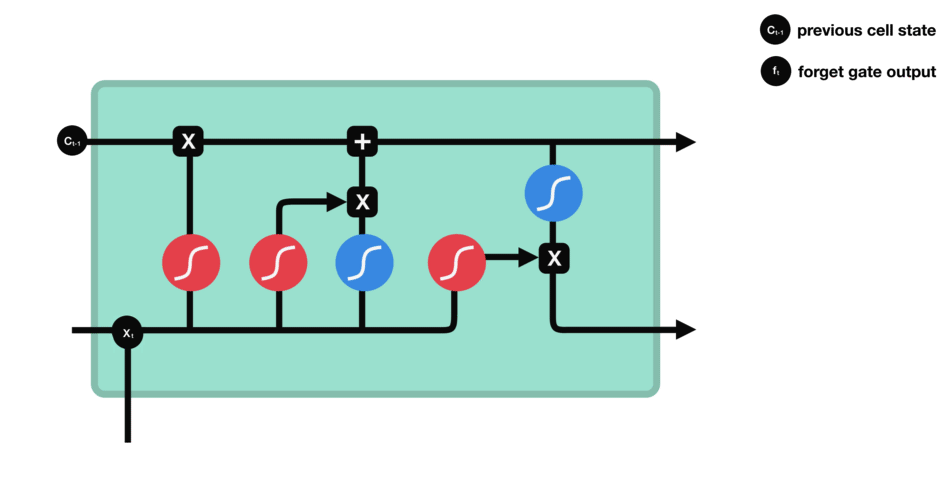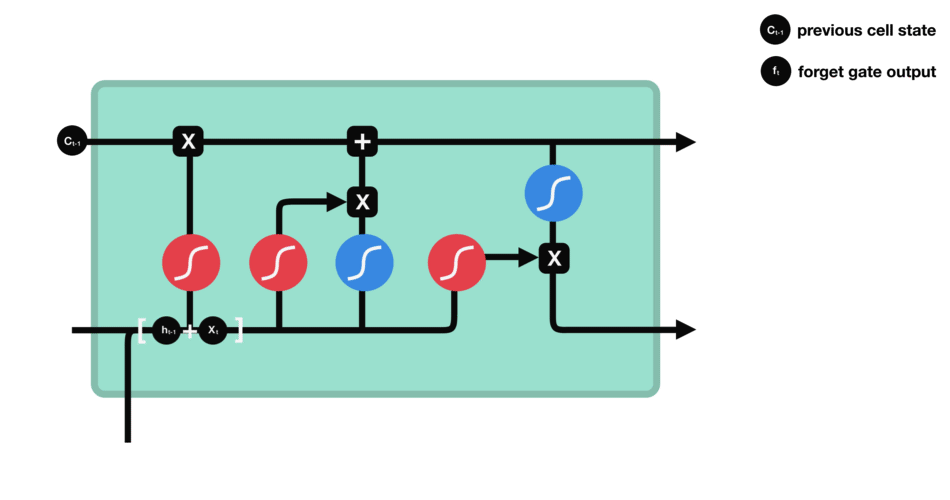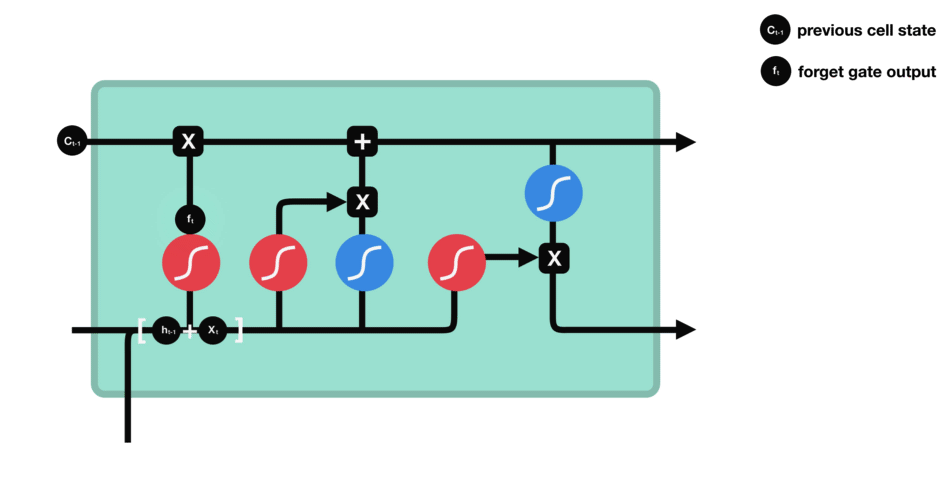
Puerta de Olvido

La puerta de olvido determina qué información del estado oculto anterior y la entrada actual debe ser retenida o descartada. Las entradas se procesan a través de una función sigmoide, produciendo valores entre 0 y 1, donde 0 indica olvido y 1 indica retención.

Puerta de Entrada

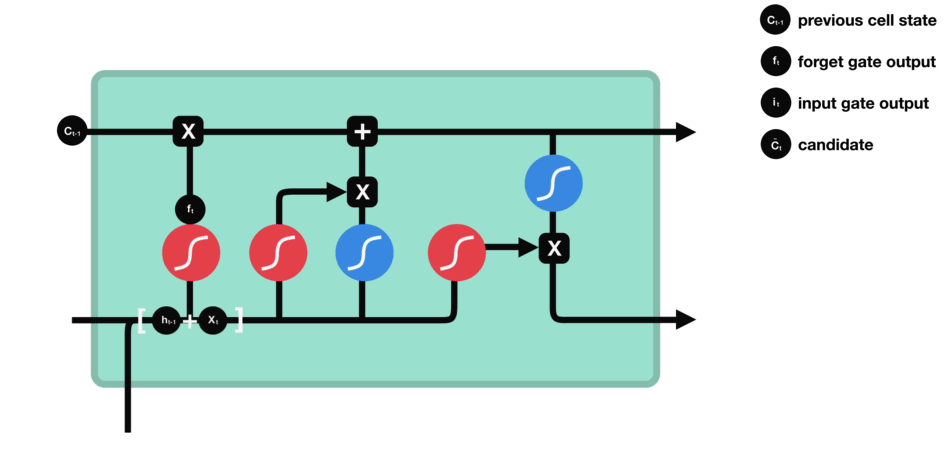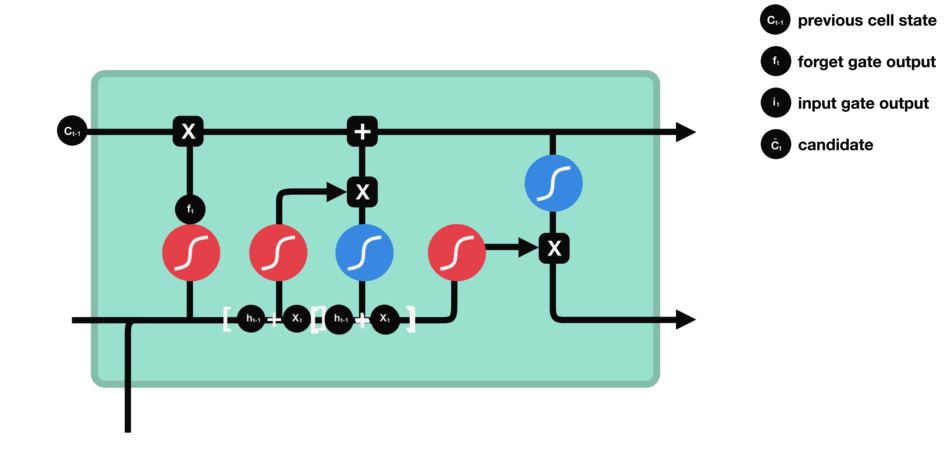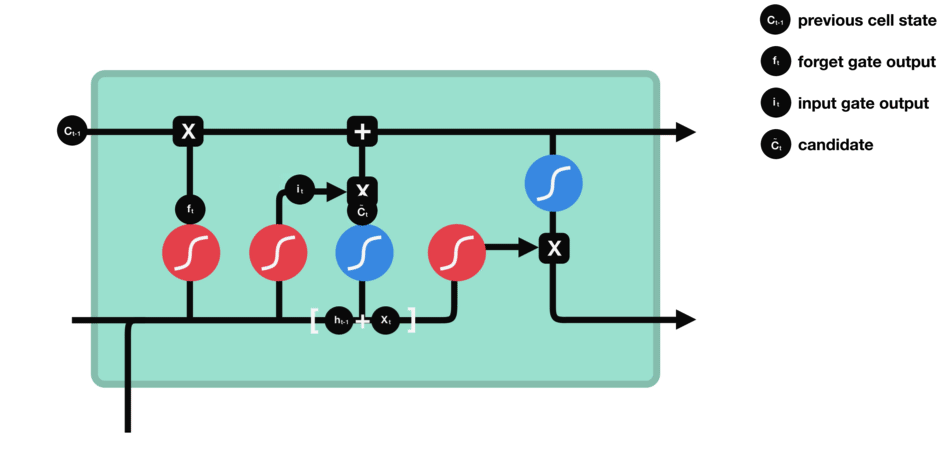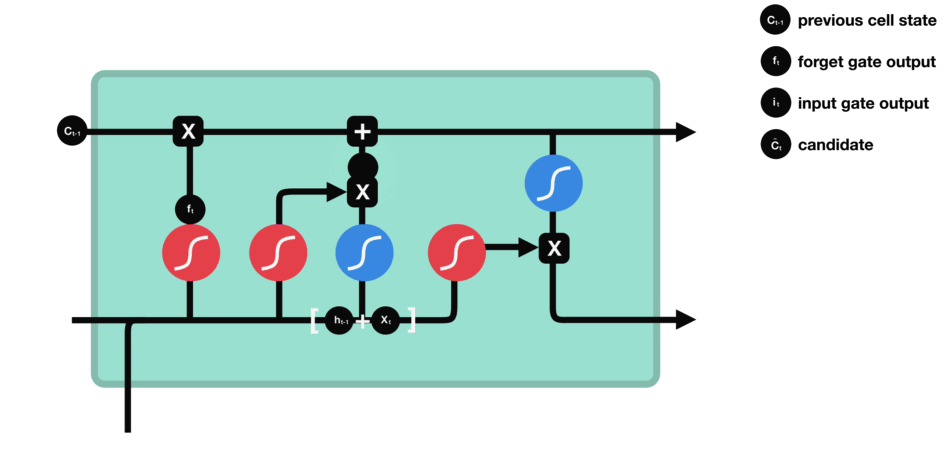
La puerta de entrada decide qué nueva información debe actualizar el estado de la celda. Combina una función sigmoide, identificando valores importantes, y una función tanh, regulando los rangos de valores. Estas salidas se multiplican para finalizar la actualización del estado de la celda.

Estado de la Celda

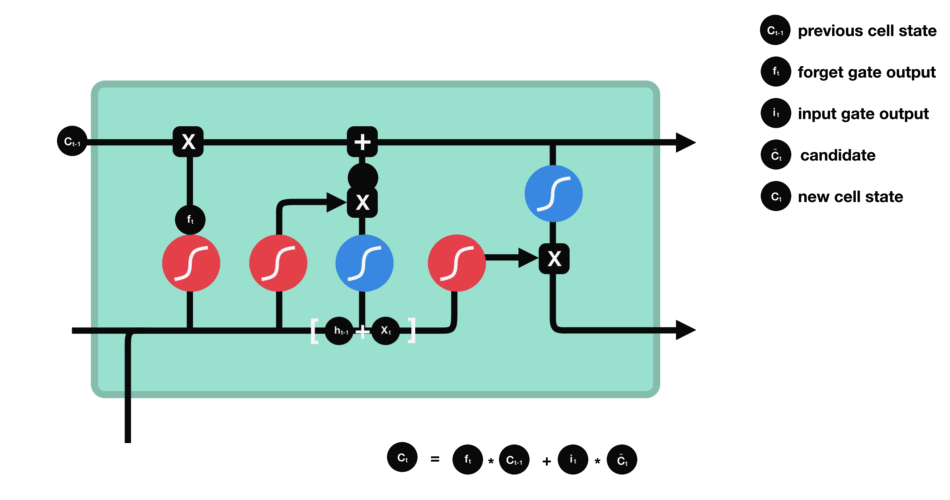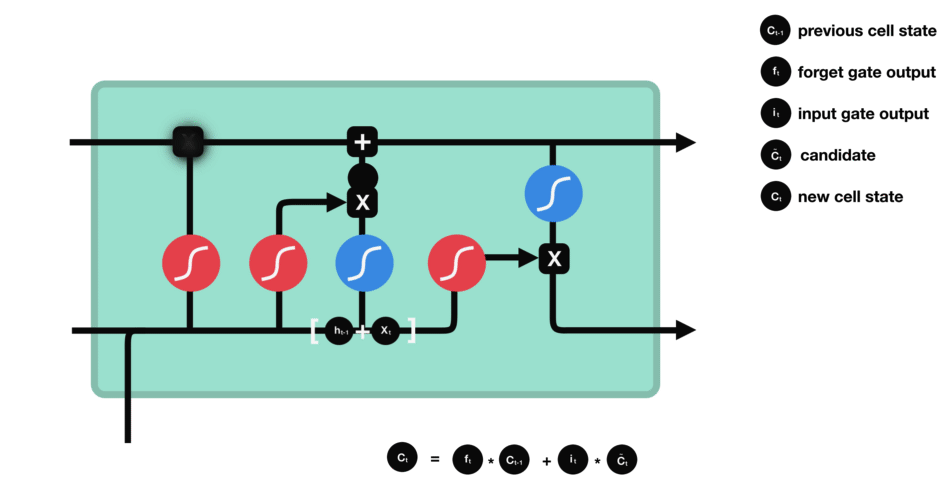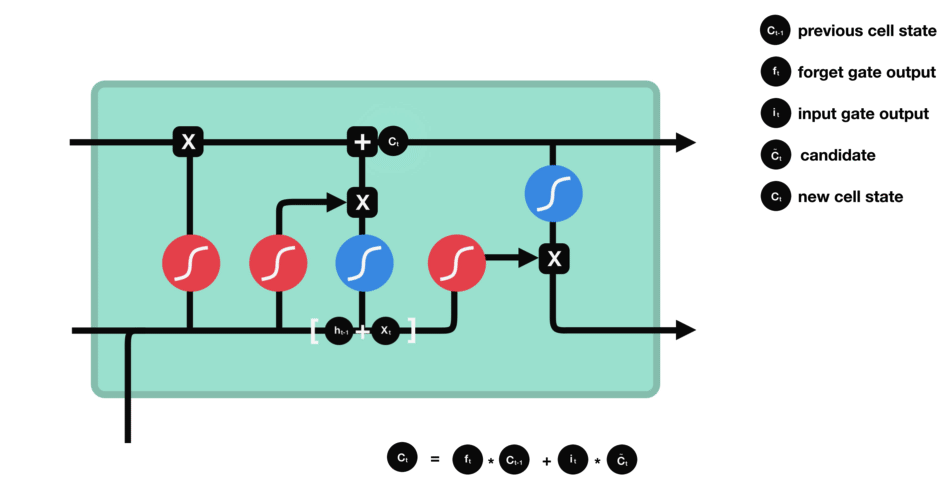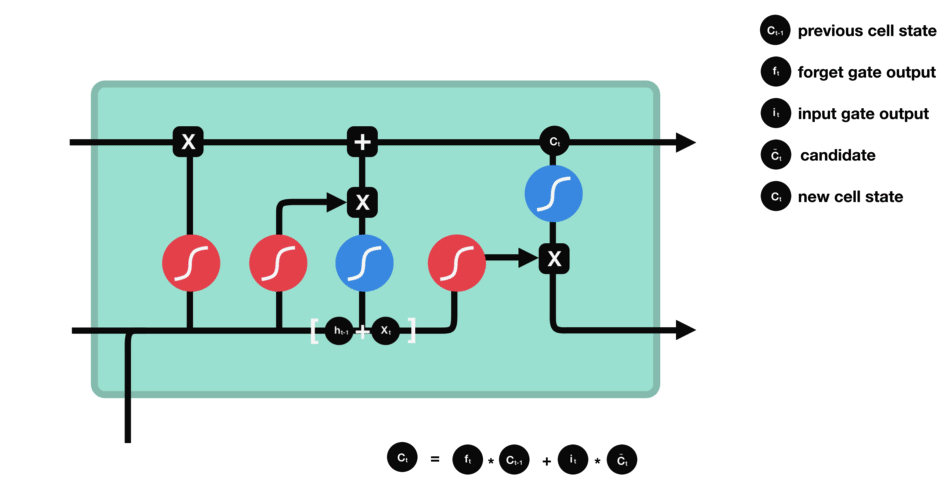
El estado de la celda se actualiza combinando las salidas de la puerta de olvido y la puerta de entrada. El estado de la celda existente se multiplica elemento por elemento por la salida de la puerta de olvido, eliminando información irrelevante. Luego, se añade información relevante de la puerta de entrada para crear el estado de la celda actualizado.

Puerta de Salida

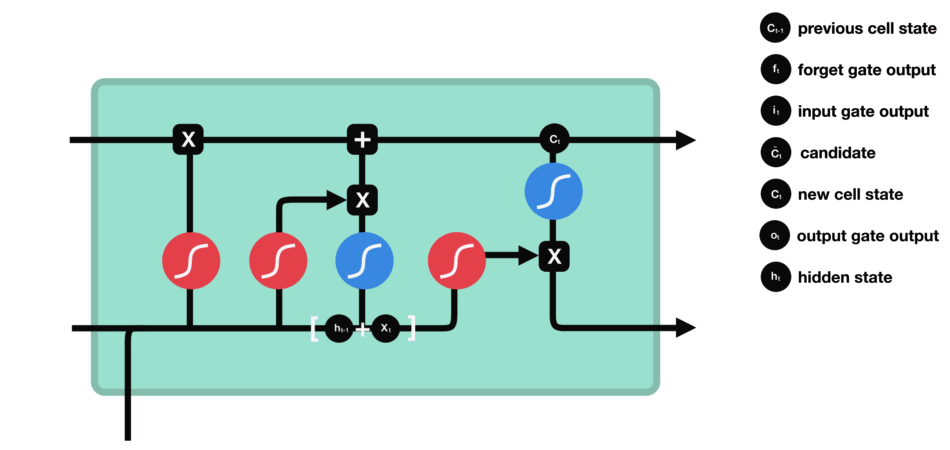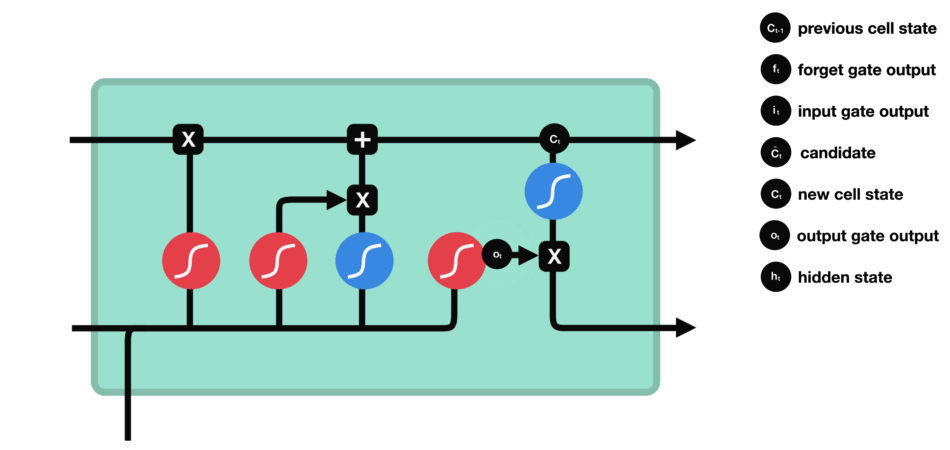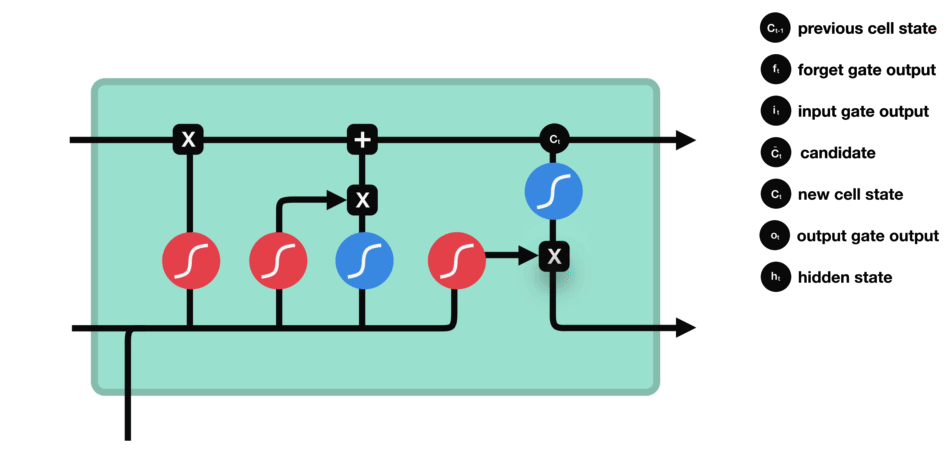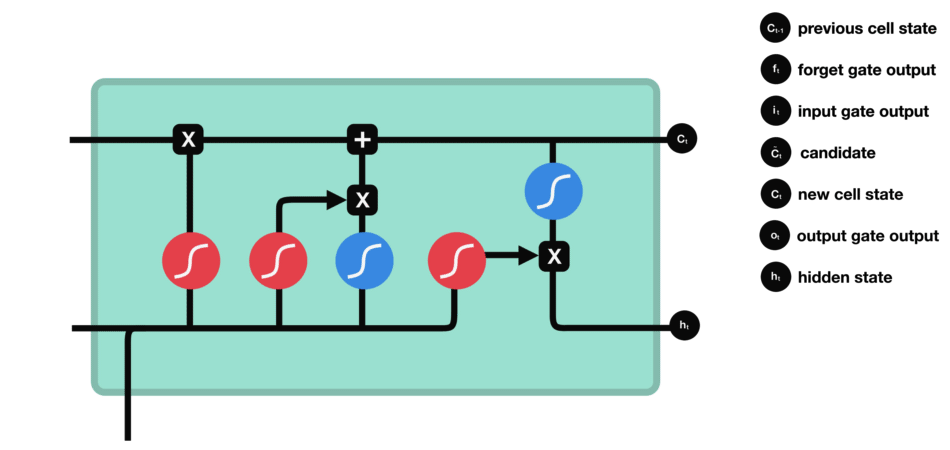
La puerta de salida define el siguiente estado oculto, decidiendo qué información retener para las predicciones. Utiliza una función sigmoide en la entrada y el estado oculto anterior, y una función tanh en el estado de la celda actualizado. Estas salidas se multiplican para generar el estado oculto final.

Los hiperparámetros son configuraciones esenciales que impactan significativamente el rendimiento de una red LSTM. A continuación, se explican los principales:

Tamaño de Ventana

Define el número de pasos de tiempo utilizados como la secuencia de entrada. Un tamaño de ventana apropiado permite al modelo capturar patrones relevantes en los datos secuenciales. Una ventana que es demasiado pequeña puede perder información importante, mientras que una ventana que es demasiado grande puede introducir ruido y aumentar la complejidad computacional.

Épocas

Representa el número de pasadas completas sobre el conjunto de datos durante el entrenamiento. Un mayor número de épocas permite que el modelo aprenda mejor, pero también aumenta el riesgo de sobreajuste. Se recomiendan técnicas como el "early stopping" para detener el entrenamiento cuando el rendimiento en los datos de validación deja de mejorar.

Tamaño del Lote

Indica el número de muestras procesadas antes de actualizar los parámetros internos del modelo. Tamaños de lote más grandes pueden llevar a pasos de gradiente más estables, mientras que tamaños más pequeños ofrecen una mayor variabilidad que puede ayudar a escapar de mínimos locales. Un valor comúnmente utilizado es 32, aunque puede ajustarse según los requisitos específicos del modelo y los recursos computacionales disponibles.

Unidades

Se refiere al número de neuronas en cada capa LSTM. Un mayor número de unidades permite al modelo capturar patrones más complejos, pero también aumenta el riesgo de sobreajuste y la carga computacional. Es crucial equilibrar la capacidad del modelo con la complejidad de la tarea y el tamaño del conjunto de datos.

Función de Activación

Las funciones de activación introducen no linealidad en el modelo, permitiéndole aprender relaciones complejas en los datos. En las capas LSTM, se utilizan comúnmente funciones como la tangente hiperbólica (tanh) o sigmoide, mientras que las capas densas a menudo emplean ReLU (Unidad Lineal Rectificada). La elección de la función de activación depende de la tarea específica y puede influir en la convergencia y el rendimiento del modelo.

Optimizador

El optimizador es el algoritmo que ajusta los pesos del modelo para minimizar la función de pérdida. Adam es ampliamente utilizado por su eficiencia y adaptabilidad, combinando los beneficios de los algoritmos AdaGrad y RMSProp. La elección del optimizador puede afectar la velocidad de convergencia y la calidad final del modelo.

Función de Pérdida

La función de pérdida cuantifica la discrepancia entre las predicciones del modelo y los valores reales. Para tareas de regresión, como la predicción de series temporales, se utiliza comúnmente el Error Cuadrático Medio (MSE), ya que penaliza grandes desviaciones y proporciona una medida clara del rendimiento del modelo.

Preparar tus datos es un paso crucial en el entrenamiento de cualquier modelo de aprendizaje automático, especialmente en redes LSTM. Un preprocesamiento adecuado asegura que los datos estén en un formato adecuado, mejorando la precisión y eficiencia del modelo. A continuación, se presentan los pasos clave en la tubería de preprocesamiento para modelos LSTM:

Paso 1: Separación de Características y Etiquetas

El primer paso consiste en separar el conjunto de datos en características y etiquetas. Las características representan los datos de entrada, mientras que las etiquetas son la salida objetivo. Este paso es esencial ya que permite que el modelo LSTM aprenda de los patrones relevantes en las características de entrada y prediga los valores futuros en las etiquetas.

Paso 2: Escalado de Datos de Entrada y Salida

Para mejorar el rendimiento del modelo, es necesario escalar los datos de entrada y salida a un rango que el modelo pueda procesar de manera eficiente. El MinMaxScaler escala todos los valores a un rango entre 0 y 1, lo que ayuda al modelo a converger más rápido y evita problemas con diferentes magnitudes de características.

Paso 3: Creación de Ventanas Deslizantes para Datos Secuenciales

Los modelos LSTM están diseñados para trabajar con datos secuenciales, por lo que crear ventanas deslizantes asegura que el modelo reciba secuencias de entrada para el entrenamiento. Este paso implica generar secuencias a partir de los datos, típicamente con un tamaño de ventana predefinido que representa el número de pasos de tiempo anteriores utilizados para predecir el siguiente valor.

Paso 4: Formato 3D para la Entrada LSTM

Los modelos LSTM esperan que los datos de entrada estén en un formato específico 3D: `[samples, timesteps, features]`. Este paso remodela los datos a este formato, donde `samples` son el número de secuencias, `timesteps` son el número de pasos de tiempo por secuencia y `features` son el número de características en cada paso de tiempo.

Por Qué el Preprocesamiento es Crucial

Un preprocesamiento adecuado es esencial para entrenar un modelo LSTM preciso y eficiente. Sin un preprocesamiento adecuado, el modelo puede tener problemas con datos ruidosos, escalado inapropiado o características irrelevantes, lo que lleva a un rendimiento deficiente. Al seguir los pasos descritos anteriormente, aseguras que los datos sean adecuados para aprender patrones complejos y hacer predicciones precisas.

Entrenar un modelo LSTM implica un proceso iterativo donde los datos se pasan a través de múltiples épocas y se dividen en lotes más pequeños. Cada época representa un pase completo por el conjunto de datos, mientras que los lotes permiten que el modelo actualice sus pesos de manera incremental. Este enfoque permite que la red generalice mejor y adapte sus parámetros de manera efectiva con el tiempo.

En el núcleo de este proceso, las capas LSTM sobresalen en la identificación de patrones temporales dentro de datos secuenciales. Al procesar las entradas un paso de tiempo a la vez, capturan dependencias a lo largo de secuencias largas, lo que las hace ideales para tareas que requieren entender el orden de los eventos o relaciones de series temporales.

Asegurar la reproducibilidad es un aspecto crítico del entrenamiento. Establecer semillas aleatorias ayuda a mantener la consistencia en la inicialización de pesos y el barajado de datos, lo que permite comparaciones justas entre diferentes experimentos o ejecuciones. Esta práctica es particularmente importante en entornos de investigación y colaboración.

A pesar de sus fortalezas, los modelos LSTM pueden encontrar desafíos durante el entrenamiento. El sobreajuste es un problema común, especialmente con datos limitados, donde el modelo aprende el ruido en lugar de los patrones subyacentes. Técnicas como dropout, regularización y detención temprana son efectivas para mitigar este problema. También pueden surgir dificultades de convergencia, particularmente en redes profundas o con hiperparámetros mal elegidos. Monitorear el proceso de entrenamiento y ajustar parámetros puede mejorar significativamente el rendimiento.